Tree:
Data frequently contain a hierarchical relationship between various elements. The data structure which reflects this relationship is called a rooted tree graph or simply a tree. Among different types of data structures in practice, tree is very important to store and manipulate data with complex relationship. This is sometimes like the properties of an object. For example, properties to store of an employee in the office directory can be name, age, sex, salary etc. Again the properties “name” can have sub-properties like first name, middle name, last name etc. This can be showed as follows.
Read More: What are the different types of Data Structures?
Types of Trees in Data Structure:
1. General Tree or Tree:
A general tree is a data structure where it is has a root and the root can have zero or any number of disjoint trees. The structure of a general tree is that, any node can be a root to any number of children and each children (nodes) can a root to any number of children. Thus the subtrees may contain any number of siblings and subtrees. Following is a general tree.
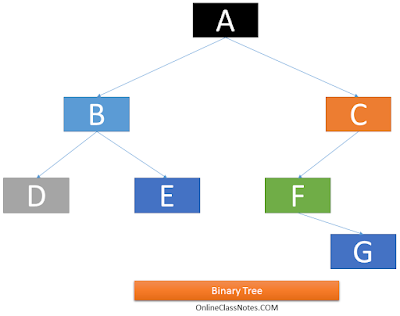
2 Binary Tree:
A binary tree is a tree which can be empty or can have a root R with at most 2 children. Each of these children then can be an empty tree or can again contain at most 2 children to form a binary tree. Following is an example of binary tree
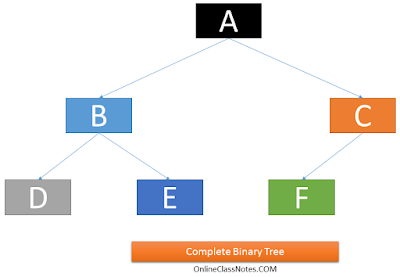
3. Complete Binary Tree:
A binary tree is said to be a complete binary tree in data structure if it meets the following conditions
- All the levels except possibly the last level have maximum number of possible nodes.
- All the nodes in the last level appear as far left as possible. That is, at the last level, there should not be any right successor of a parent not without a left successor
For example, the above given figure of Binary Tree is not a Complete Binary Tree because the last level starts with no left children of D, even if D and E were having 2 children each, still it could not be a Complete Binary Tree as because F doesn’t have a left successor. Following is an example of complete binary tree
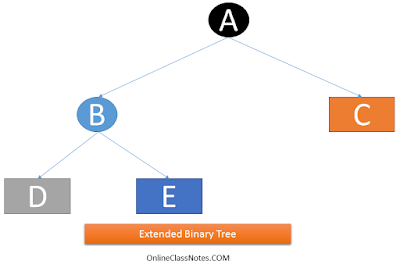
4. Extended Binary Tree or 2 Trees:
A Binary Tree is called an Extended Binary Tree if each of its nodes are containing either 0 or 2 child nodes. A node with no children is a dead end to travel, thus it is called an external node, and a node with children is called an internal node. Also, in diagrams, the internal nodes are marked with circles and external nodes are marked with squares. Following is an Extended Binary Tree
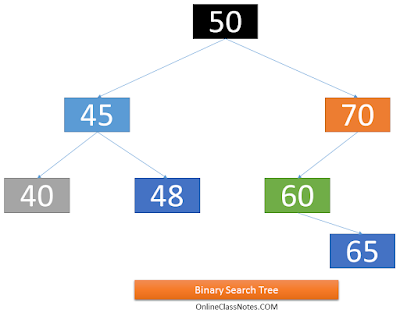
5. Binary Search Trees or Binary Sorted Tree:
A Binary Tree is called an Binary Search Tree when value of each node is greater than any value of its left subtree and less than any value of its right subtree. However when the tree may contain duplicates, then the definition changes a little as value of each node is greater than any value of its left subtree and less than or equal to any value of its right subtree. Following is an example of Binary Search Tree
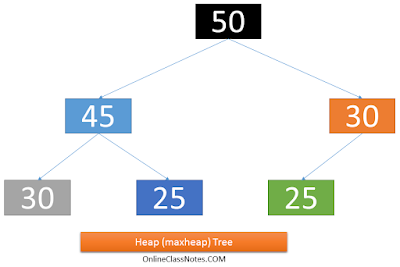
6. Heap Tree:
A Complete Binary Tree is called an Heap (Maxheap) when value of any node N is greater than or equal to the value of any child node of N. Analogously, a minheap is a heap tree where value of any node N is less than or equal to the value of any child node of N. Following is an example of Heap Tree